کتاب Mathematical Logic and Computation (منطق و محاسبات ریاضی) از جدیدترین منابع یادگیری ریاضیات و منطق آن میباشد. این کتاب در 17 بخش به بررسی مسائل مختلف ریاضیات خواهد پرداخت.
در ادامه مقدمهای از کتاب Mathematical Logic and Computation را از زبان نویسنده شرح خواهیم داد.
مقدمهای بر کتاب Mathematical Logic and Computation:
در عبارت منطق ریاضی، کلمه “ریاضی” مبهم است. میتوان روشهای مورد استفاده را مشخص کرد، به طوری که این عبارت به مطالعه ریاضی اصول استدلال اشاره دارد. میتوان نوع استدلال در نظر گرفته را مشخص کرد، به طوری که این عبارت به مطالعه استدلال ریاضی خاص اشاره دارد. یا میتوان آن را برای نشان دادن هدف در نظر گرفت، به طوری که این عبارت به مطالعه منطق با نگاهی به کاربردهای ریاضی اشاره دارد.
در عنوان کتاب Mathematical Logic and Computation، کلمه “ریاضی” به دو معنای اول در نظر گرفته شده است، اما به معنای سوم نیست. به عبارت دیگر، منطق ریاضی در اینجا به عنوان مطالعه ریاضی روشهای استدلال ریاضی در نظر گرفته میشود. موضوع در نوع خود جالب است و کاربردهای ریاضی دارد. اما در علوم رایانه نیز کاربردهایی دارد، به عنوان مثال، برای تأیید سخت افزار و نرم افزار و مکانیزه کردن استدلال ریاضی. این میتواند با ارائه مدلهای ایدهآل از معنای انجام ریاضیات، فلسفه ریاضیات را نیز آگاه کند.
چیزی که منطق را به عنوان یک رشته متمایز میکند تمرکز آن بر زبان است. موضوع با عبارات رسمی شروع میشود که قرار است زبان غیر رسمی را که ما برای تعریف اشیا، بیان ادعاها و اثبات آنها استفاده میکنیم، مدل کنند.
در آن نقطه، دو دیدگاه متمایز ظاهر میشود. از منظر معنایی، عبارات رسمی برای بیان چیزهایی در مورد اشیاء و ساختارهای ریاضی انتزاعی استفاده میشود. آنها میتوانند برای مشخص کردن کلاسهایی از ساختارها مانند گروهها، حلقهها و زمینهها استفاده شوند. برای مشخص کردن ساختارهای خاص، مانند صفحه اقلیدسی یا اعداد واقعی. یا برای توصیف روابط درون یک ساختار خاص. از این منظر، منطق ریاضی علم ارجاع، تعریف پذیری و صدق است که مفاهیم معنایی را که رابطه بین زبان ریاضی و ساختارهای ریاضی توصیف شده را تعیین میکند، روشن میکند.
کتاب Mathematical Logic and Computation دیدگاه نحوی تری را اتخاذ میکند که در آن موضوعات اصلی مورد علاقه خود عبارات هستند. از این منظر، از زبانهای رسمی برای استدلال و محاسبه استفاده می شود و آنچه ما به آن اهمیت میدهیم قوانینی است که بر استفاده صحیح آنها حاکم است. ما از سیستمهای رسمی برای درک الگوهای استنتاج ریاضی و ساختار تعاریف و اثباتهای ریاضی استفاده خواهیم کرد و به کارهایی که میتوانیم با این نمایشهای نحوی انجام دهیم علاقه مند خواهیم بود.
ما از استفاده از روشهای معنایی دوری نخواهیم کرد، اما هدف ما استفاده از معناشناسی برای روشن کردن نحو است نه برعکس. دلایل متعددی وجود دارد که چرا رویکرد نحوی ارزشمند است. نظریه ریاضی نحو به طور مستقل جالب و آموزنده است. تمرکز بر اشیاء نحوی نیز بیشتر با علوم کامپیوتر همسو میشود، زیرا این اشیاء را میتوان بهعنوان داده نشان داد و توسط الگوریتمها بر روی آنها عمل کرد. در نهایت، مزایای فلسفی وجود دارد.
از آنجایی که یک نظریه کلی از رشتههای محدود نمادها تمام چیزی است که برای کار با عبارات مورد نیاز است، دیدگاه نحوی ابزاری برای مطالعه استدلال ریاضی – از جمله استفاده از اشیاء و روشهای بی نهایت – بدون وارد کردن پیشفرضهای ریاضی قوی در ابتدا فراهم میکند.
یکی دیگر از ویژگیهای قابل توجه کتاب Mathematical Logic and Computation تمرکز آن بر محاسبات است. از یک طرف، ما انتظار داریم که ریاضیات درک مفهومی گستردهای به ما بدهد. در مرزهای تجربی موضوع، این امر به سازماندهی و توضیح مشاهدات علمی ما کمک میکند، اما تمایل ما برای درک به پدیدههای تجربی محدود نمیشود.
از سوی دیگر، ما همچنین از ریاضیات انتظار داریم که به ما بگوید چگونه مسیرها و احتمالات را محاسبه کنیم تا بتوانیم پیشبینیها و تصمیمگیریهای بهتری داشته باشیم و در جهت تأمین اهداف عملگرایانه خود منطقی عمل کنیم. بین درک مفهومی و محاسبه تنش وجود دارد: محاسبات مهم است، اما ما اغلب با سرکوب کردن جزئیات محاسباتی بیشتر میبینیم و به نحو مؤثرتری استدلال میکنیم.
تنش تا حدی با تمایز منطق دان بین منطق کلاسیک از یک سو و منطق شهودی یا سازنده از سوی دیگر تسخیر میشود. منطق کلاسیک به معنای حمایت از سبکی از استدلال است که از انتزاع و ایده آل سازی پشتیبانی می کند، در حالی که منطق شهودی مستقیماً برای تفسیر محاسباتی مناسب است.
امروزه ریاضیات قاطعانه کلاسیک است، اما ریاضیات بدون محاسبه تقریباً یک تناقض در شرایط است. و در حالی که هدف نهایی علوم کامپیوتر محاسبات عملی است، انتزاع برای طراحی و استدلال در مورد سیستمهای محاسباتی ضروری است. در اینجا ما هم منطق کلاسیک و هم منطق سازنده را با نگاهی به درک روابط بین این دو مطالعه خواهیم کرد.
ارتباط بین منطق و محاسبات عمیق است: ما میتوانیم با عبارات رسمی محاسبه کنیم، میتوانیم به طور رسمی در مورد محاسبات استدلال کنیم، و میتوانیم محتوای محاسباتی را از مشتقات رسمی استخراج کنیم. سبک ارائهای که من در اینجا اتخاذ کردهام این خطر را دارد که توسط دانشمندان کامپیوتر بیش از حد ریاضی ارزیابی شود و برای ریاضیدانان محض بیش از حد محاسباتی باشد، اما هدف من ایجاد تعادل و نزدیکتر کردن این دو جامعه است.
مخاطبین مطالب در اینجا باید در سطح پیشرفته لیسانس یا مقطع کارشناسی ارشد در دسترس باشد. من سعی کردهام ارائه را مستقل نگه دارم، اما تاکید بر اثبات چیزهایی در مورد سیستمهای منطقی است تا نشان دادن و ایجاد انگیزه در استفاده از آنها.
خوانندگانی که قبلاً با منطق آشنا شدهاند، میتوانند مطالب اینجا را سریعتر و راحت تر مرور کنند. علامتگذاری بیشتر نمادهای کتاب Mathematical Logic and Computation متعارف هستند، اما هنگام کنار هم قرار دادن مطالب از زمینههایی که قراردادها در آنها متفاوت است، چالشها ناگزیر به وجود می آیند.
بارزترین نمونه چنین چالشی، استفاده از کلاسورهایی مانند کمیکنندهها و انتزاع لامبدا است: منطقدانان ریاضی معمولاً چنین عملیاتی را محکم میگیرند، در حالی که دانشمندان رایانه معمولاً وسیعترین دامنه ممکن را به آنها میدهند. عدم تطابق دیگر با توجه به کاربرد تابع به وجود می آید، زیرا دانشمندان نظری کامپیوتر اغلب به جای f (x) f x می نویسند. بنابراین، جایی که یک منطقدان ریاضی مینویسد
یک دانشمند کامپیوتر ممکن است بنویسد:
به عنوان یک مصالحه، کتاب Mathematical Logic and Computation از نماد ریاضیدان برای منطق نمادین استفاده میکند، اما از قراردادهای دانشمند کامپیوتر برای سیستمهای محاسباتی مانند حساب لامبدا که به سادگی تایپ میشود، استفاده میکند. تفاوتها در فصلهای 14 و 17 کتاب Mathematical Logic and Computation، جایی که منطق و نظریه نوع در کنار هم قرار میگیرند، بیشتر مشهود است.
آموزش از مطالب کتاب Mathematical Logic and Computation میتوان برای تدریس تعدادی دروس مختلف استفاده کرد و وابستگی بین موضوعات خفیف است. فصلهای 1-7 مقدمهای کامل بر نحو و معناشناسی منطق مرتبه اول ارائه میکنند.
ریاضیدانان کلاسیک میتوانند به راحتی هر چیزی را که مربوط به منطق شهودی باشد، تنظیم کنند، در حالی که دانشمندان کامپیوتر و سایر افراد علاقهمند میتوانند زمان بیشتری را با آن بگذرانند. نادیده گرفتن منطق شهودی ممکن است زمان را برای قضیه حذف برش و کاربردهای آن باقی بگذارد، در حالی که نادیده گرفتن حذف برش ممکن است زمان را برای پرداختن به معناشناسی جبری باقی بگذارد.
برای دانشآموزانی که قبلاً با منطق گزارهها و منطق مرتبه اول آشنا هستند، فصلهای 8 تا 14 کتاب Mathematical Logic and Computation ارائهای نسبتاً مستقل از قضایای حساب رسمی، محاسبهپذیری و ناقص بودن ارائه میدهند.
دورهای در مورد محاسبهپذیری و ناقص بودن میتواند با فصل 8 شروع شود، بخش 8.5 را رها کنید، به فصل 11 کتاب Mathematical Logic and Computation ادامه دهید، برای پیشزمینه تعریفپذیری حسابی به بخشهای 10.2 و 10.5 مراجعه کنید، بخشهای 11.8 و 11.9 را رد کنید و سپس به فصل 12 بروید.
یک دوره در تئوری اثبات میتواند بر قضیه حذف برش و کاربردهای آن (فصل 6 و 7) و حساب لامبدا با تایپ ساده (فصل 13) تمرکز کند. فصل 14 میتواند به عنوان تمرکز یک دوره در مورد تفسیرهای محاسباتی محاسبات، بر اساس مواد در فصلهای 8-11 و 13 باشد. برای این منظور، بخشهای 8.5، 9.5، 10.6-10.7، و 11.6-11.9 کتاب Mathematical Logic and Computation را میتوان حذف کرد.
به طور مشابه، فصل 16 کتاب Mathematical Logic and Computation میتواند به عنوان کانونی برای مقدمهای بر زیرسیستمهای ریاضیات مرتبه دوم و ریاضیات معکوس باشد که توسط یک تور سریع از فصلهای 8-11 و بخشهای 15.4 و 15.5 پشتیبانی میشود. بخش 11.8 و 11.9، به ویژه، با در نظر گرفتن فصل 16 نوشته شده است.
بیشتر مطالب بعد از فصل 7 کتاب Mathematical Logic and Computation به هیچ سیستم قیاسی خاصی وابسته نیست. کسر طبیعی گاهی اوقات به طور پیشفرض استفاده میشود، اما این انتخاب برای نمایش ضروری نیست.
سرفصلهای کتاب Mathematical Logic and Computation:
- Preface
- Acknowledgments
- 1 Fundamentals
- 1.1 Languages and Structures
- 1.2 Inductively Defined Sets
- 1.3 Terms and Formulas
- 1.4 Trees
- 1.5 Structural Recursion
- 1.6 Bound Variables
- 2 Propositional Logic
- 2.1 The Language of Propositional Logic
- 2.2 Axiomatic Systems
- 2.3 The Provability Relation
- 2.4 Natural Deduction
- 2.5 Some Propositional Validities
- 2.6 Normal Forms for Classical Logic
- 2.7 Translations Between Logics
- 2.8 Other Deductive Systems
- 3 Semantics of Propositional Logic
- 3.1 Classical Logic
- 3.2 Algebraic Semantics for Classical Logic
- 3.3 Intuitionistic Logic
- 3.4 Algebraic Semantics for Intuitionistic Logic
- 3.5 Variations
- 4 First-Order Logic
- 4.1 The Language of First-Order Logic
- 4.2 Quantifiers
- 4.3 Equality
- 4.4 Equational and Quantifier-Free Logic
- 4.5 Normal Forms for Classical Logic
- 4.6 Translations Between Logics
- 4.7 Definite Descriptions
- 4.8 Sorts and Undefined Terms
- 5 Semantics of First-Order Logic
- 5.1 Classical Logic
- 5.2 Equational and Quantifier-Free Logic
- 5.3 Intuitionistic Logic
- 5.4 Algebraic Semantics
- 5.5 Definability
- 5.6 Some Model Theory
- 6 Cut Elimination
- 6.1 An Intuitionistic Sequent Calculus
- 6.2 Classical Sequent Calculi
- 6.3 Cut-Free Completeness of Classical Logic
- 6.4 Cut Elimination for Classical Logic
- 6.5 Cut Elimination for Intuitionistic Logic
- 6.6 Equality
- 6.7 Variations on Cut Elimination
- 6.8 Cut-Free Completeness of Intuitionistic Logic
- 7 Properties of First-Order Logic
- 7.1 Herbrand’s Theorem
- 7.2 Explicit Definability and the Disjunction Property
- 7.3 Interpolation Theorems
- 7.4 Indefinite Descriptions
- 7.5 Skolemization in Classical Theories
- 8 Primitive Recursion
- 8.1 The Primitive Recursive Functions
- 8.2 Some Primitive Recursive Functions and Relations
- 8.3 Finite Sets and Sequences
- 8.4 Other Recursion Principles
- 8.5 Recursion along Well-Founded Relations
- 8.6 Diagonalization and Reflection
- 9 Primitive Recursive Arithmetic
- 9.1 A Quantifier-Free Axiomatization
- 9.2 Bootstrapping PRA
- 9.3 Finite Sets and Sequences
- 9.4 First-Order PRA
- 9.5 Equational PRA
- 10 First-Order Arithmetic
- 10.1 Peano Arithmetic and Heyting Arithmetic
- 10.2 The Arithmetic Hierarchy
- 10.3 Subsystems of First-Order Arithmetic
- 10.4 Interpreting PRA
- 10.5 Truth and Reflection
- 10.6 Conservation Results via Cut Elimination
- 10.7 Conservation Results via Model Theory
- 11 Computability
- 11.1 The Computable Functions
- 11.2 Computability and Arithmetic Definability
- 11.3 Undecidability and the Halting Problem
- 11.4 Computably Enumerable Sets
- 11.5 The Recursion Theorem
- 11.6 Turing Machines
- 11.7 The Lambda Calculus
- 11.8 Relativized Computation
- 11.9 Computability and Infinite Binary Trees
- 12 Undecidability and Incompleteness
- 12.1 Computability and Representability
- 12.2 Incompleteness via Undecidability
- 12.3 Incompleteness via Self-Reference
- 12.4 The Second Incompleteness Theorem
- 12.5 Some Decidable Theories
- 13 Finite Types
- 13.1 The Simply Typed Lambda Calculus
- 13.2 Strong Normalization
- 13.3 Confluence
- 13.4 Combinatory Logic
- 13.5 Equational Theories
- 13.6 First-Order Theories and Models
- 13.7 Primitive Recursive Functionals
- 13.8 Propositions as Types
- 14 Arithmetic and Computation
- 14.1 Realizability
- 14.2 Metamathematical Applications
- 14.3 Modified Realizability
- 14.4 Finite-Type Arithmetic
- 14.5 The Dialectica Interpretation
- 15 Second-Order Logic and Arithmetic
- 15.1 Second-Order Logic
- 15.2 Semantics of Second-Order Logic
- 15.3 Cut Elimination
- 15.4 Second-Order Arithmetic
- 15.5 The Analytic Hierarchy
- 15.6 The Second-Order Typed Lambda Calculus
- 15.7 Higher-Order Logic and Arithmetic
- 16 Subsystems of Second-Order Arithmetic
- 16.1 Arithmetic Comprehension
- 16.2 Recursive Comprehension
- 16.3 Formalizing Analysis
- 16.4 Weak Konig’s Lemma
- 16.5 1 Comprehension and Inductive Definitions
- 16.6 Arithmetic Transfinite Recursion
- 17 Foundations
- 17.1 Simple Type Theory
- 17.2 Mathematics in Simple Type Theory
- 17.3 Set Theory
- 17.4 Mathematics in Set Theory
- 17.5 Dependent Type Theory
- 17.6 Inductive Types
- 17.7 Mathematics in Dependent Type Theory
- Appendix Background
- A.1 Naive Set Theory
- A.2 Orders and Equivalence Relations
- A.3 Cardinality and Zorn’s Lemma
- A.4 Topology
- A.5 Category Theory
- References
- Notation
- Index
جهت دانلود کتاب Mathematical Logic and Computation میتوانید پس از پرداخت، دریافت کنید.


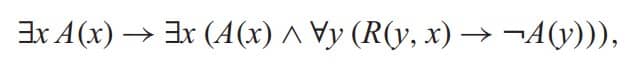
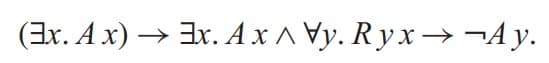
دیدگاهها
هیچ دیدگاهی برای این محصول نوشته نشده است.